Luogu_P8742题解

欢迎收看CooooldWind的题解

本题是洛谷P8742

思路

众所周知的，这是能载入史册的经典的“01背包”题，适合刚入门的同学们做。

本题目的状态转移方程需要满足：

1. 不放砝码，即上面的方案都能用；
2. 在对于第 个砝码的选择中选择左边，即砝码重量加现在的天平上的重量等于原来的重量；
3. 在对于第 个砝码的选择中选择右边，即砝码重量减现在的天平上的重量等于原来的重量。

为了防止你们看不懂，我做了个图。

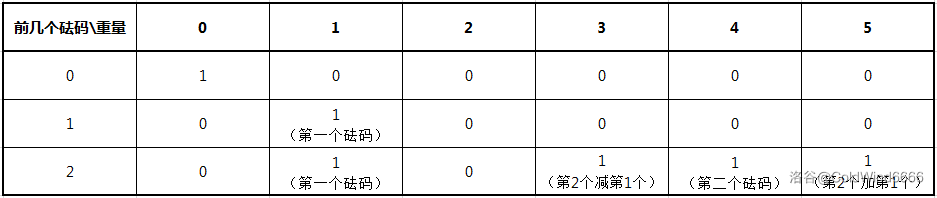
*从此处到“思路”内容结束以下为2023.9.22添加内容。

为了防止你们连图都看不懂，我就细说一波。

这张图使用的样例输入如下：

2
1 4

我们设 为当前砝码的重量。

在开始正式的说明之前，我们最好加一个限制条件：如果天平两侧都没有砝码，放砝码的时候只能放在左边。只有这样子，后面的砝码才能根据第一个砝码加减计算。

所以关于第一个砝码，我们可以不放，也可以放。

但是到了第二个砝码，如果第一个不放：

1. 把这个砝码放在左边（因为上面说了，整个天平在这个时候没有砝码），此时称量 重量的物品；

2. 不放，此时称量重量为 的物品。

如果第一个被放了呢？那又是：

1. 放在左边，此时称量 重量的物品；

2. 放在右边，此时称量 重量的物品；

3. 不放，此时称量 重量的物品。

所以总共有 ， ， ， 以及 五种，但是世界上没有没重量的物质啊，所以其实只有4种，分别为 ， ， ， 。

以及，为什么要求最大值为所有砝码重量之和，并且在以下代码的内循环使用呢？因为最大只能称那么多，设到 （至少对于我的代码而言）丝毫没有用。

最后，本题为了节省空间复杂度（不大规范的简而言之，就是存的数据的数量，各位有想细细了解的欢迎咨询百度），可以使用一维数组迭代。请各位自行尝试，本题解不做讲解。

代码

#include<bits/stdc++.h>
using namespace std;
int n,w[1500],w_max,ans;
bool dp[1500][120000];
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++){
        cin >> w[i];
        w_max = w_max + w[i]; //把所有砝码都加起来就是最大值
    }
    /*
    双重循环，遍历dp。
    由于里面有dp[i][j] = dp[i - 1][j]，所以就不需要考虑什么没有质量的情况了。
    上一行dp[0][0] = 1被我删掉了，原因也是如此。
    */
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= w_max;j++){
            /*
            这里面的 if-else 结构可以换成
            “dp[i][j] = dp[i - 1][j] || w[i] == j || dp[i - 1][j + w[i]] || dp[i - 1][abs(j - w[i])];”
            */
            //不放砝码，即上面的方案都能用。
            dp[i][j] = dp[i - 1][j];
            
            //只放现在的那个。
            if(w[i] == j) dp[i][j] = 1; 
            
            //在对于第 i 个砝码的选择中选择左边，即砝码重量加现在的天平上的重量等于原来的重量。
            else if(dp[i - 1][j + w[i]] == 1) 
                dp[i][j] = 1; 
                
            //在对于第 i 个砝码的选择中选择右边，即砝码重量减现在的天平上的重量等于原来的重量。
            else if(dp[i - 1][abs(j - w[i])] == 1) 
                dp[i][j] = 1; 
                
            //计算总数。
            if(dp[n][j] == 1) ans++;
        }
    }
    cout << ans;
    return 0;
}